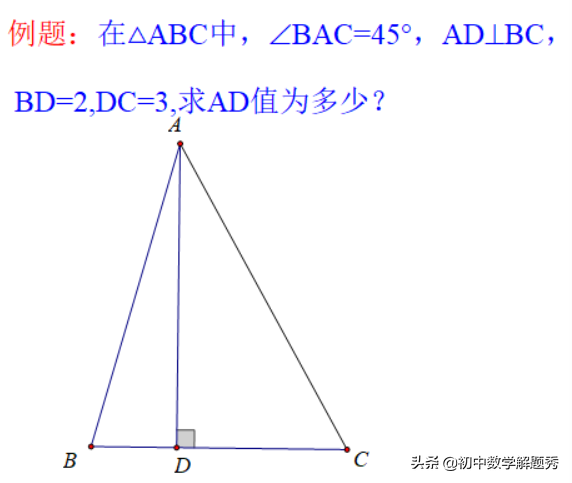
先来审题:本题有个“好角”45°,快速检索思维,围绕这个45°可以做点什么事情呢?思维风暴:①本题高中方法来做,可以直接用两角和的正切公式,最便捷;②见到45°联想“正方形中的45°模型”将这个图形补成正方形,继而勾股定理计算;③考虑到BC=5所对的∠BAC=45°,联想到“定弦定角必有隐圆”模型,可以构造辅助圆解题;④构造“一线三等角”模型,再构造两个45°和∠BAC相等,利用相似解题。本题方法多多,先来展示上述思路。
方法1:构造“正方形中的45°”模型。这个模型内涵丰富,可用旋转等方法证明,在此不表。本题中,巧用结论中的2组全等,把条件收缩集中到直角三角形BCF中,利用勾股定理计算即可,如图:

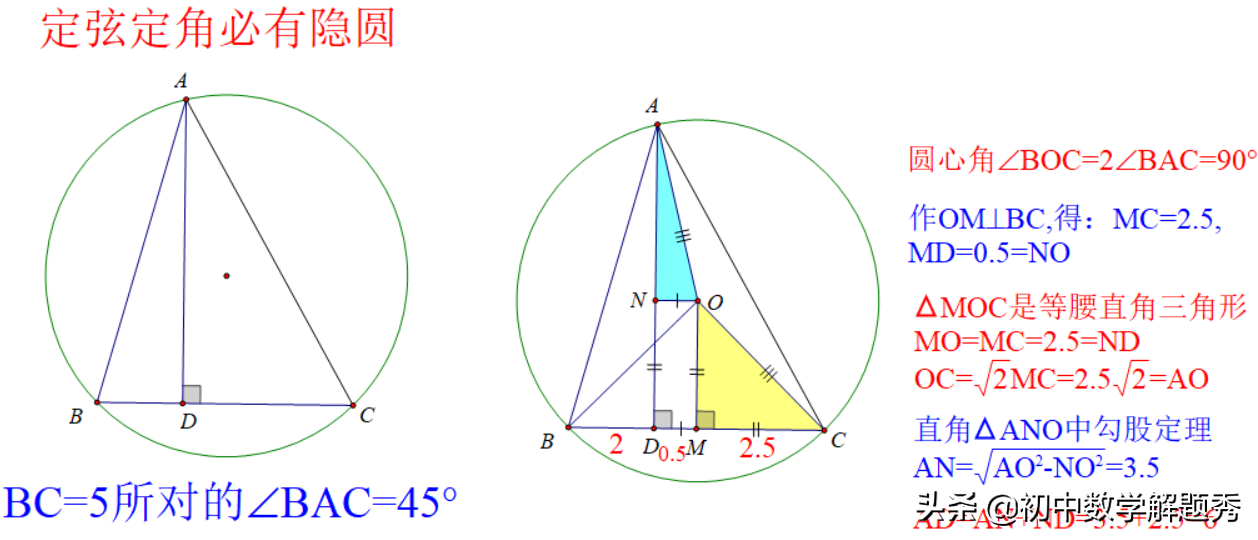
方法2:构造"定弦定角必有隐圆”模型。圆心角∠BOC=2∠BAC=90°,△MOC是等腰直角三角形求出MO=MC=ND,和半径OC,然后直角三角形△ANO中勾股定理求出AN即可。如图:
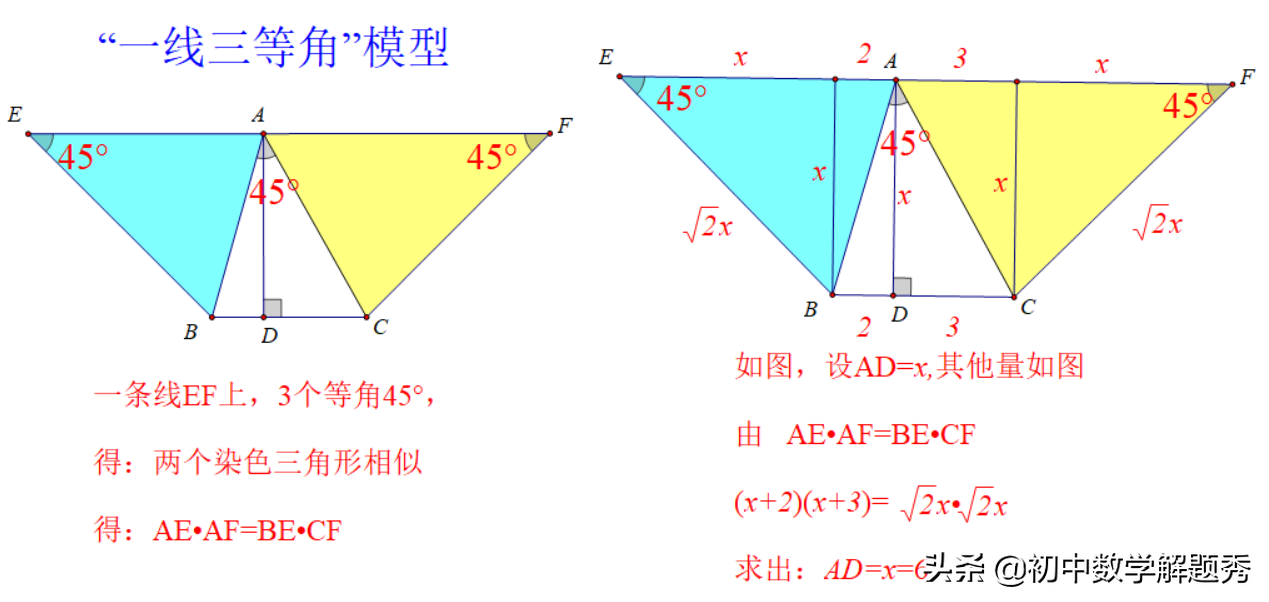
方法3:构造“一线三等角”相似模型。相似证明本文不展开,只点明思路技巧。再结合45°角的特殊性,构造出两个等腰直角三角形,设AD=x表示出其他线段,最后通过相似结论AE•AF=BE•CF列出方程计算即可,如图:
当然了,本题还可用两角和的正切公式,非常干净利落。在此也提供给初中学生欣赏一下,公式证明待到高中会详细学习,在此不表。如图:

本题经典,平中见奇,方法精彩,简约不凡,值得好好品味研究,欢迎收藏分享评点!