逆向思维,一种非常普遍的思考方式。在解答初中数学压轴题时,我们可以运用逆向思维从问题去寻找答案,这种解题方法通常是横着走的存在。那么,何时运用逆向思维?为什么运用逆向思考?怎么运用逆向思考?下面,以几道经典的数学例题做一个详细的解析!
一、从顺、逆两个方面去理解概念
例1:若化简|1-x|-|x-4|的结果为2x-5,求x的取值范围。
【分析】:原式=|1-x|-|x-4|
根据题意,要化成:x-1-(4-x)=2x-5
从绝对值概念的反方向考虑,推出其条件是:
1-x≤0,且x-4≤0
∴x的取值范围是:1≤x≤4
再者,例如我们在教学“倒数”概念时,不但可以问学生:“4的倒数是什么”?还可以问“-1/2是什么数的倒数”?“-7和什么数互为倒数”?互为倒数的两个数有何特征”?等问题,从而帮助学生更加深刻理解倒数概念。
二、从顺、逆两个方面去掌握公式、法则和定律
数学中的许多公式、法则和定律都可用等式表示,等式具有双向性,既可以用左边的式子替换右边的式子,也可以用右边的式子替换左边的式子。
例1:若a+b+c=0
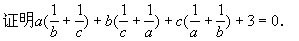
【分析】:先把求证的等式左边的“ 3”写成“ 1+1+1”,再逆用分配律,本题即可得证。
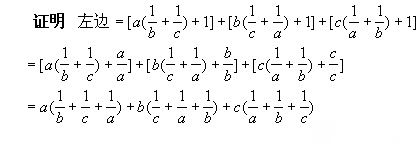
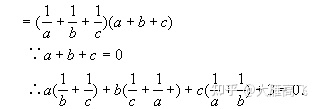
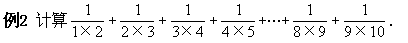
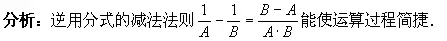
(练习题)下列各题,如不逆用积的乘方法则,势必感到束手无策。
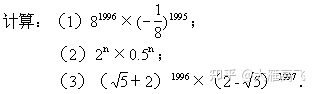
三、解题中注意逆向思维的训练
在解题时,一般都是由所给条件直接向结论逼近。对于以下题目,从反面去考虑,可能会获得更为简捷的解题方法,我们平时要加强这种方法的训练。
例1:解方程
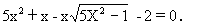
【分析】:解方程(组)时,一般需将多元化为一元,然后求解。但上述方程去根号后将得高次方程,求解困难。若逆向考虑增元,即设√5x²-1=y(y≥0),于是,原方程变为y2-xy+x-1=0,左边分解因式,得(y-1)(y-x+1)=0。从而解的y=1或者y=x-1,√5x²-1==1或√5x²-1=x-1,由此很容易求出x。
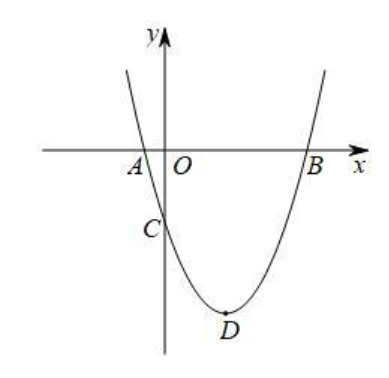
例2: 如图,已知抛物线y=x-3x-1.75的顶点为D,并与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C。
(1)求点A,B,C,D的坐标。
(2)取点E(-1.5,0)和点F(0,-0.75),直线L经过E,F两点,点G是线段BD的中点。
①判断点G是否在直线L上,请说明理由。
②在抛物线上是否存在点M,使点M关于直线L的对称点在x轴上?若存在,求出点M的坐标;若不存在,请说明理由。
【分析】第(1)问:依旧是送分题,求点的坐标,方程、公式、配方,十年未变!
第(2)问①:判断点是否在直线上,求出直线的解析式,将点的横坐标代入,再判断是否等于纵坐标即可。对于程度一般的学生,亦可轻松秒杀!
第(2)问②:传说中的压轴题,顺向思考,求出直线L的解析式,设M的坐标(m,m-3m-1.75),然后做关于L的对称点,构造全等三角形求出对称点的坐标,最后判断纵坐标是否等于0。一顿操作之后,发现1个小时过去了。如果是平时练习,尚有商量的余地。如果在中考中,估计还没等到求出坐标,考试结束的铃声已经响起!
那么,这个时候就应该清楚,碰到这种类型的题目,是时候用逆向思考了。
第一,先判断已知点的特殊性,发现直线EF中的E点刚好在x轴上,而G刚好是线段BD的中点,且BD⊥EF,那么B、D关于直线L对称。
第二、由于两点确定一条直线,即得直线ED与x轴关于直线L对称。所以,题目所求的M点即为直线ED与抛物线的交点。
四、编排逆向训练的习题
为了训练学生的逆向思维,在教学中,要有意识地编排顺、逆双向配对的练习题供学生训练。
3的绝对值是__;__的绝对值是3; 2的平方是__;4是__的平方根。
如果α+β=180°,那么α与β____;如果α与β互为补角,α+β=____。
通过以上题目我们发现,只需要我们在平时多问一些问什么?遇到一个命题或者结论,我们不妨进行逆向思考,多想问题的反面是否成立,考虑其逆命题是否成立,或许你就会有意外的收获。
事实上,逆向思维的培养是提高学生思维能力的一个重要方面。逆向思维是一种发散思维,是从原问题的相反方向、否定方向或已有思路的相反方向进行思考的一种思维,即“由果索因、知本求源”。